- 之前介绍的方法都是 value-based 的方法,从这章开始时基于 policy-based 的方法。
- policy function approximation 是直接建立一个基于策略的目标函数来进行梯度上升的优化。
将基于表格表示的策略 转换为 基于函数表示的策略。
即此时策略 π 可以描述为:
π(a∣s,θ)
其中,θ∈Rm表示参数向量,是我们需要进行优化的。
- 当策略是以表格的形式保存时,我们定义最优的策略为 在该策略下的所有 state value 都是最大的。
- 当策略是以函数的形式存在时,我们定义 最优的策略 为 可以最大化一个确定的常数指标(certain scalar metrics).
Policy gradient 的基本步骤:
- 确定 metrics/objective function,来定义最优的策略:J(θ)
- 进行优化,如梯度上升算法
θt+1=θt+α▽θJ(θt)
vˉπ=s∈S∑d(s)vπ(s)=dTvπ
- vˉπ 显然是 state value 的加权平均。
- d(s)≥0 是各个 state 的权重
- ∑s∈Sd(s)=1, 我们可以认为 d(s) 是 概率分布,因此该指标可以描述为:
vˉπ=ES∼d[vπ(S)]
J(θ)=E[t=0∑∞γtRt+1]
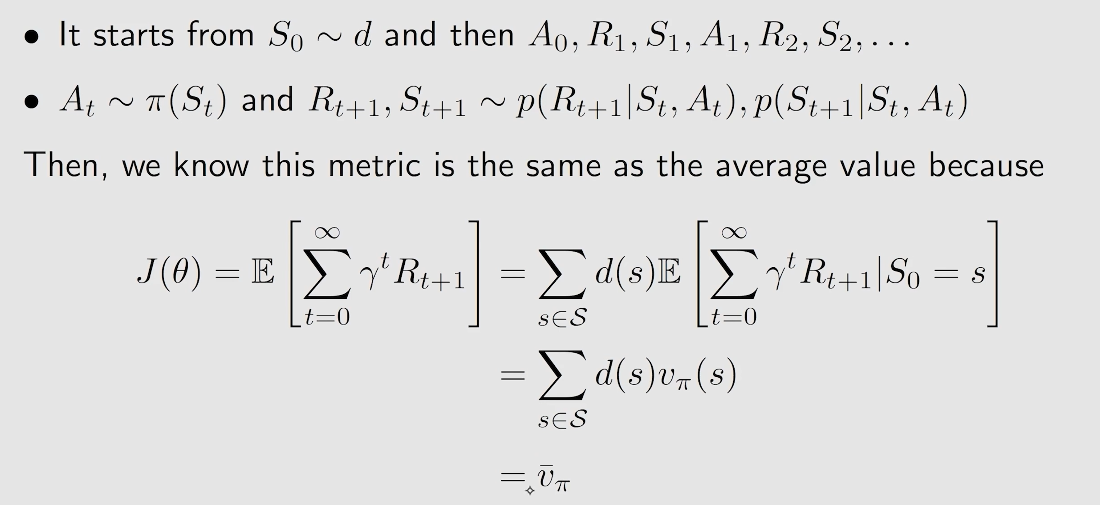 20240826173749
20240826173749d 与策略 π 无关
这种情况我们将 d 表示为 d0, vˉπ 表示为 vˉπ0.
这种情况下的 d 可以根据对各个状态的重要程度进行选择:
一种是将所有状态视为同等重要,一种则是有所偏向。
d 与策略 π 有关 d 表示为 dπ(s), 即在策略 π 下的 stationary distribution。
rˉπ=s∈S∑dπ(s)rπ(s)=ES∼d[rπ(s)]
其中:
rπ(s)r(s,a)≐a∈A∑π(a∣s)r(s,a)=E[R∣s,a]=r∑rp(r∣s,a)
rπ(s)表示在策略π下 状态s时可以得到的平均reward。
r(s,a)表示在单步情况下(在状态s采用动作a)时的平均reward。
假设 agent 跟随一个 给定的策略 然后生成了一个 trajectory以及对应的 rewards (Rt+1,Rt+2,…)
对应 average single-step reward along this trajectory is
====n→∞limn1E[Rt+1+Rt+2+⋯+Rt+n∣St=s0]n→∞limn1E[k=1∑nRt+k∣St=s0]n→∞limn1E[k=1∑nRt+k]s∑dπ(s)rπ(s) rˉπ
这里在视频没有详细介绍,只给出了梯度的公式:
▽θJ(θ)=s∈S∑η(s)a∈A∑▽θπ(a∣s,θ)qπ(s,a)=E[▽θlnπ(A∣S,θ)qπ(S,A)]
其中
- J(θ) 可以是 vˉπ, rˉπ, vˉπ0 任何一种。
- "=" 有表示 严格等于 近似 以及 成比例等于
- η 表示 state 的权重或者分布
具体推导过程:
▽θlnπ(a∣s,θ)▽θJ(θ)=π(a∣s,θ)▽θπ(a∣s,θ)=s∈S∑d(s)a∈A∑▽θπ(a∣s,θ)qπ(s,a)=s∈S∑d(s)a∈A∑π(a∣s,θ)▽θlnπ(a∣s,θ)qπ(s,a)=ES∼d[a∑π(s∣S,θ)▽θlnπ(a∣S,θ)qπ(S,a)]=ES∼d, A∼π[▽θlnπ(A∣S,θ)qπ(S,A)]≐E[▽θlnπ(A∣S,θ)qπ(S,A)]
根据这个式子我们就可以通过 SGD 方法,从而可以进行近似求解:
▽θJ(θ)≈▽θlnπ(a∣s,θ)qπ(s,a)
一些特性 这里的策略是随机性 的,因为我们需要计算的是 lnπ(a∣s,θ), 因此我们需要保证对于所有的 s,a,θ
π(a∣s,θ)≥0
 20240826180244
20240826180244梯度上升算法的本质就是最大化目标函数 J(θ)
θt+1=θt+α▽θJ(θ)=θt+αE[▽θlnπ(A∣S,θt)qπ(S,A)]
而对应的真实梯度可以用一个估计的梯度来替代:
θt+1=θt+α▽θlnπ(at∣st,θt)qπ(s,a)
但还存在 qπ(s,a) 是未知的,我们也可以进行近似:
θt+1=θt+α▽θlnπ(a∣s,θt)qt(st,at)
这里可以用不同的方法来近似 qπ(s,a).
- Monte-Carlo based method, 我们便称为 REINFORCE
- 也可以采用基于 TD 的算法 或者 其他的算法。
一些细节
 20240826181340
20240826181340 20240826181538
20240826181538 20240826181638
20240826181638 20240826181712
20240826181712