对于 q-value 的估计从 基于表格的 (tabular representation) 转换到 基于函数的 (function representation)
- 通过使用一个函数来进行拟合 state values 或者 action values: v^(s,w)≈vπ(s), 其中w∈Rm是参数向量。
- 可以提高存储效率
- 提高泛化能力
目标: 寻找一个最优的参数w,使得v^(s,w)最接近真实的vπ(s).
共两步:
J(w)=E[(vπ(S)−v^(S,w))2]
分析随机变量 S 的 probability distribution (即对于损失函数中的 expection 需要考虑怎样对状态进行平均):
认为所有状态都是同等重要的,即各个状态的可能性为∣S∣1 因此这种情况下的 objective function 可以写成:
J(w)=E[(vπ(S)−v^(S,w))2]=∣S∣1s∈S∑(vπ(s)−v^(s,w))2
但实际情况可能并不是所有状态的概率都是一致的,基于给定策略下,一些状态可能很少被访问,另一些则频繁被访问,因此采用这种 objective function 就不太可行。
- stationary: 表示是一种长时间的交互行为
- distributon: 表示是 状态 的分布
- 通常也称为 steady-state distributon or limiting distributon.
describes the long-run behavior of a Markov process. 即基于一个策略,我们不断地与环境进行交互,最终会达到一个平稳的状态,此时可以分析每一个状态在这个策略下的概率。
设 {dπ(s)}s∈S 表示 基于策略 π 下的 stationary distribution。其中 dπ(s)≥0 且 ∑s∈Sdπ(s)=1
那么此时的 objective function 可以表示为:
J(w)=E[(vπ(S)−v^(S,w))2]=s∈S∑dπ(s)(vπ(s)−v^(s,w))2
 20240820181406
20240820181406 20240820181718
20240820181718目前的优化算法只是在估计给定策略的 state value
minisize obejctive function J(w), 采用 梯度下降 算法:
wk+1=wk−αk▽wJ(wk)
对应目标函数的真实梯度是:
▽wj(w)=▽wE[(vπ(S)−v^(S,w))2]=E[▽w(vπ(S)−v^(S,w))2]=−2E[(vπ(S)−v^(S,w))▽wv^(S,w)]
这里包含了一个 Expection,因此可以考虑 SGD 方法进行求解:
wk+1=wk+αk(vπ(st)−v^(st,wt))▽wvt^(st,wt)
其中st是随机变量S的一个样本。
但这里还有一个难点,vπ(st) 我们是无法估计的,这是我们所求的量,因此需要用近似算法来进行替代,从而使得算法可行。
设 gt 表示在一个 episode 中,从状态 st 出发的 discounted return。因此我们用 gt 来近似 vπ(st), 即:
wk+1=wk+αk(gt−v^(st,wt))▽wvt^(st,wt)
在 TD 算法中,我们将 rt+1+γv^(st+1,wt) 来近似 vπ(st), 因此对应算法为:
wk+1=wk+αk(rt+1+γv^(st+1,wt)−v^(st,wt))▽wvt^(st,wt)
wk+1=wk+αk(rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt))▽wqt^(st,at,wt)
 20240820184127
20240820184127wk+1=wk+αk(rt+1+γa∈A(st+1)maxq^(st+1,at+1,wt)−q^(st,at,wt))▽wqt^(st,at,wt)
on-policy版本:
 20240820184405
20240820184405Deep Q-learning 目的是最小化目标函数(objective/loss function):
J(w)=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
其中 (S,A,R,S′) 均是随机变量。
采用梯度下降。
J(w)=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
对于 q^(S,A,w) 求解梯度还是很好求的。
但对于 maxa∈A(S′)q^(S′,a,w) 其求解梯度比较难求,在 DQN 中采用一个 固定 的方法进行解决。
尝试将 y≐R+γmaxa∈A(S′)q^(S′,a,w) 中的 w 进行固定求解,具体如下:
引入两个网络:
main network q^(s,a,w)
w 会一直进行更新,根据梯度下降的公式。
target network q^(s′,a,wT)
并不是一直进行更新,而是等 main network 更新一定次数后,将该网络的 w 复制到 wT 中
将 objective function 修改为:
J(w)=E[(R+γa∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))2]
在计算 main network q^(s,a,w) 的梯度时,将 q^(S′,a,wT) 中的 wT 固定不动,因此左侧那个类似 TD target 的就不是有关 w 的函数,不用进行求导,从而方便计算。
然后在更新了一定次数之后,在将 wT=w 进行赋值。
因此对应的损失函数的梯度可以修改为:
▽wJ=E[−2(R+γa∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))▽wq^(S,A,w)]=E[−2(YT−q^(S,A,w))▽wq^(S,A,w)]
一些细节:
- w 和 wT 表示 the main and target networks 的参数,在初始化的时候是设为相同的。
- 在每一次迭代时,我们需要从经验池 (the replay buffer) 中取出一定数量的样本 (a mini-batch of samples {(s,a,r,s')}) 进行训练。
- 网络的输入包括 状态 s 和 动作 a. 在训练求解梯度时,我们先直接求解 target network 的输出,视为 yT≐r+γmaxa∈A(s′)q^(s′,a,wT)。
然后我们通过 mini-batch 样本 {(s,a,yT)}, 通过梯度的算法来最小化对应的损失函数, 假设有 N 个样本,那么对应的损失函数求解为:J(w)=i=1∑NyT−q^(s,a,w)
即可以通过梯度下降,来更新参数值wt+1=wt+αtN1i=1∑N(yT−q^(si,ai,wt))⋅▽wq^(si,ai,wt)
 20240820230827
20240820230827 20240820230920
20240820230920 20240820230944
20240820230944 20240820231024
20240820231024但在发表 DQN 的文章中,不太一样,在原文是 on-policy 且 main network 的输出是不一样的。
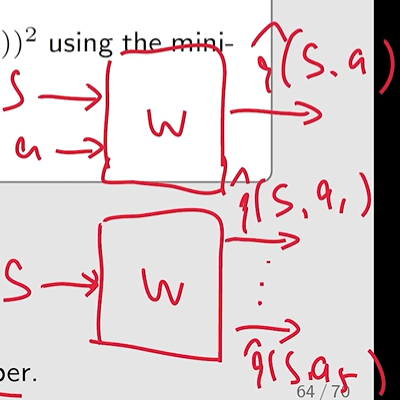 20240820231205
20240820231205








