state value the Bellman equation 引入随机变量后对应的discounted return的描述。
S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , S t + 2 → A t + 3 … S_t\overset{A_t}{\rightarrow}R_{t+1},S_{t+1}\overset{A_{t+1}}{\rightarrow}R_{t+2},S_{t+2}\overset{A_{t+2}}{\rightarrow}R_{t+3},S_{t+2}\overset{A_{t+3}}{\rightarrow}\dots S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , S t + 2 → A t + 3 …
对应的discounted return为:G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + … G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\dots G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + …
γ \gamma γ G t G_t G t State value 是 G t G_t G t G t G_t G t
v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s) = E[G_t|S_t=s] v π ( s ) = E [ G t ∣ S t = s ]
是一个有关状态s的函数. v π ( s ) v_\pi(s) v π ( s ) π \pi π state value 可以用来衡量一个状态的价值. Return 是针对一条trajectory所求的,而 State value 则是对多个 trajectory 求 return 再求平均值。π ( a ∣ s ) , p ( r ∣ s , a ) , p ( s ′ ∣ s , a ) \pi(a|s),p(r|s,a),p(s'|s,a) π ( a ∣ s ) , p ( r ∣ s , a ) , p ( s ′ ∣ s , a )
用来描述所有状态的state value的关系.
S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , S t + 2 → A t + 3 … S_t\overset{A_t}{\rightarrow}R_{t+1},S_{t+1}\overset{A_{t+1}}{\rightarrow}R_{t+2},S_{t+2}\overset{A_{t+2}}{\rightarrow}R_{t+3},S_{t+2}\overset{A_{t+3}}{\rightarrow}\dots S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , S t + 2 → A t + 3 …
对应的 discounted return G t G_t G t
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + … = R t + 1 + γ ( R t + 2 + γ R t + 3 + … ) = R t + 1 + γ G t + 1 \begin{aligned} G_{t} & =R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \\ & =R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) \\ & =R_{t+1}+\gamma G_{t+1} \end{aligned} G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + … = R t + 1 + γ ( R t + 2 + γ R t + 3 + … ) = R t + 1 + γ G t + 1
因此,对应的 state value 为:
v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] \begin{aligned} v_\pi(s) & =E[G_t|S_t=s] \\ & = E[R_{t+1}+\gamma G_{t+1}|S_t=s] \\ & = \color{blue}{E[R_{t+1}|S_t=s]} \color{black}{+} \color{blue}{\gamma E[G_{t+1}|S_t=s]} \end{aligned} v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ]
需要推导E [ R t + 1 ∣ S t = s ] E[R_{t+1}|S_t=s] E [ R t + 1 ∣ S t = s ] E [ G t + 1 ∣ S t = s ] E[G_{t+1}|S_t=s] E [ G t + 1 ∣ S t = s ]
E [ R t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) E [ R t + 1 ∣ S t = s , A t = a ] = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r \begin{aligned} E[R_{t+1}|S_t=s] & = \sum_a \pi(a|s)E[R_{t+1}|S_t=s,A_t=a] \\ & =\sum_a \pi(a|s) \sum_r p(r|s,a)r \end{aligned} E [ R t + 1 ∣ S t = s ] = a ∑ π ( a ∣ s ) E [ R t + 1 ∣ S t = s , A t = a ] = a ∑ π ( a ∣ s ) r ∑ p ( r ∣ s , a ) r
E [ G t + 1 ∣ S t = s ] = ∑ s ′ E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = ∑ s ′ E [ G t + 1 ∣ S t + 1 = s ′ ] ( 无记忆性 ) = ∑ s ′ v π ( s ′ ) p ( s ′ ∣ s ) = ∑ s ′ v π ( s ′ ) ∑ a p ( s ′ ∣ s , a ) π ( a ∣ s ) \begin{aligned} E[G_{t+1}|S_t=s] & = \sum_{s'}E[G_{t+1}|S_t=s,S_{t+1}=s'] \\ & =\sum_{s'}E[G_{t+1}|S_{t+1}=s'] (无记忆性) \\ & =\sum_{s'}v_\pi(s')p(s'|s) \\ & =\sum_{s'}v_\pi(s')\sum_a p(s'|s,a)\pi(a|s) \end{aligned} E [ G t + 1 ∣ S t = s ] = s ′ ∑ E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = s ′ ∑ E [ G t + 1 ∣ S t + 1 = s ′ ] ( 无记忆性 ) = s ′ ∑ v π ( s ′ ) p ( s ′ ∣ s ) = s ′ ∑ v π ( s ′ ) a ∑ p ( s ′ ∣ s , a ) π ( a ∣ s )
个人推导:
E [ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) E [ G t + 1 ∣ S t = s , A t = a ] = ∑ a π ( a ∣ s ) ∑ s ′ E [ G t + 1 ∣ S t = s , A t = a , S t + 1 = s ′ ] = ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) E [ G t + 1 ∣ S t + 1 = s ′ ] = ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) \begin{aligned} E[G_{t+1}|S_t=s] & = \sum_{a}\pi(a|s)E[G_{t+1}|S_t=s,A_t=a] \\ & = \sum_{a}\pi(a|s)\sum_{s'}E[G_{t+1}|S_t=s,A_t=a,S_{t+1}=s'] \\ & = \sum_{a}\pi(a|s)\sum_{s'}p(s'|s,a)E[G_{t+1}|S_{t+1}=s'] \\ & = \sum_{a}\pi(a|s)\sum_{s'}p(s'|s,a)v_\pi(s') \end{aligned} E [ G t + 1 ∣ S t = s ] = a ∑ π ( a ∣ s ) E [ G t + 1 ∣ S t = s , A t = a ] = a ∑ π ( a ∣ s ) s ′ ∑ E [ G t + 1 ∣ S t = s , A t = a , S t + 1 = s ′ ] = a ∑ π ( a ∣ s ) s ′ ∑ p ( s ′ ∣ s , a ) E [ G t + 1 ∣ S t + 1 = s ′ ] = a ∑ π ( a ∣ s ) s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ )
v π ( s ) = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] , = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r ⏟ mean of immediate rewards + γ ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ⏟ mean of future rewards , = ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ] , ∀ s ∈ S . \begin{aligned} v_{\pi}(s) & =\mathbb{E}\left[R_{t+1} | S_{t}=s\right]+\gamma \mathbb{E}\left[G_{t+1} | S_{t}=s\right], \\ & =\underbrace{\sum_{a} \pi(a | s) \sum_{r} p(r | s, a) r}_{\text {mean of immediate rewards }}+\underbrace{\gamma \sum_{a} \pi(a | s) \sum_{s^{\prime}} p\left(s^{\prime} | s, a\right) v_{\pi}\left(s^{\prime}\right)}_{\text {mean of future rewards }}, \\ & =\sum_{a} \pi(a | s)\left[\sum_{r} p(r | s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} | s, a\right) v_{\pi}\left(s^{\prime}\right)\right], \quad \forall s \in \mathcal{S} . \end{aligned} v π ( s ) = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] , = mean of immediate rewards a ∑ π ( a ∣ s ) r ∑ p ( r ∣ s , a ) r + mean of future rewards γ a ∑ π ( a ∣ s ) s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ ) , = a ∑ π ( a ∣ s ) [ r ∑ p ( r ∣ s , a ) r + γ s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ ) ] , ∀ s ∈ S .
该式子针对状态空间中的所有状态均成立. 通过 Bootstrapping , 可以求解 state value. π ( a ∣ s ) \pi(a|s) π ( a ∣ s ) p ( r ∣ s , a ) , p ( s ′ ∣ s , a ) p(r|s,a),p(s'|s,a) p ( r ∣ s , a ) , p ( s ′ ∣ s , a ) s s s
v π ( s ) = r π ( s ) + γ ∑ s ′ p π ( s ′ ∣ s ) v π ( s ′ ) \begin{aligned} v_\pi(s)=r_\pi(s)+\gamma\sum_{s'}p_{\pi}(s'|s)v_\pi(s') \end{aligned} v π ( s ) = r π ( s ) + γ s ′ ∑ p π ( s ′ ∣ s ) v π ( s ′ )
将所有状态的 Bellman equation 整合,重新修改为 matrix-vector form.
v π = r π + γ P π v π \begin{aligned} \color{blue}{v_\pi=r_\pi+\gamma P_\pi v_\pi} \end{aligned} v π = r π + γ P π v π
其中,
v π = [ v π ( s 1 ) , … , v π ( s n ) ] T ∈ R n v_\pi=[v_\pi(s_1),\dots,v_\pi(s_n)]^T\in R^n v π = [ v π ( s 1 ) , … , v π ( s n ) ] T ∈ R n r π = [ r π ( s 1 ) , … , r π ( s n ) ] T ∈ R n r_\pi=[r_\pi(s_1),\dots,r_\pi(s_n)]^T\in R^n r π = [ r π ( s 1 ) , … , r π ( s n ) ] T ∈ R n P π ∈ R n × n P_\pi\in R^{n\times n} P π ∈ R n × n [ P π ] i j = p π ( s j ∣ s i ) [P_\pi]_{ij}=p_\pi(s_j|s_i) [ P π ] ij = p π ( s j ∣ s i ) 为了进行 Policy evaluation , 即对于给定策略,求出其对应状态的 state value 的过程。 通过 Bellman euqation 进行求解。
The closed-form solution(不常用): v π = ( I − γ p π ) − 1 r π \begin{aligned} v_\pi=(I-\gamma p_\pi)^{-1}r_\pi \end{aligned} v π = ( I − γ p π ) − 1 r π
An iterative solution(一种迭代策略): v k + 1 = r π + γ P π v k \begin{aligned} v_{k+1}=r_\pi+\gamma P_\pi v_k \end{aligned} v k + 1 = r π + γ P π v k
可以最开始均初始化为 0 , 然后进行不断迭代,可以得到一个序列v 0 , v 1 , v 2 , … {v_0,v_1,v_2,\dots} v 0 , v 1 , v 2 , … v k → v π = ( I − γ p π ) − 1 r π , k → ∞ v_k \rightarrow v_\pi=(I-\gamma p_\pi)^{-1}r_\pi,\space k\rightarrow\infty v k → v π = ( I − γ p π ) − 1 r π , k → ∞
State value: agent从一个状态出发可以得到的平均return.from a state Action value: agent从一个状态出发,采取一个指定的action可以得到的平均return。a state and taking an action . 通过求解 action value 我们可以分析出在该状态下采取哪个 action 收益最大.
q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] \begin{aligned} q_\pi(s,a)=E[G_t|S_t=s,A_t=a] \end{aligned} q π ( s , a ) = E [ G t ∣ S t = s , A t = a ]
同样地,q π ( s , a ) q_\pi(s,a) q π ( s , a ) π \pi π
E [ G t ∣ S t = s ] ⏟ v π ( s ) = ∑ a E [ G t ∣ S t = s , A t = a ] ⏟ q π ( s , a ) π ( a ∣ s ) \underbrace{\mathbb{E}\left[G_{t} | S_{t}=s\right]}_{v_{\pi}(s)}=\sum_{a} \underbrace{\mathbb{E}\left[G_{t} | S_{t}=s, A_{t}=a\right]}_{q_{\pi}(s, a)} \pi(a | s) v π ( s ) E [ G t ∣ S t = s ] = a ∑ q π ( s , a ) E [ G t ∣ S t = s , A t = a ] π ( a ∣ s )
因此,v π ( s ) = ∑ a q π ( s , a ) π ( a ∣ s ) v_\pi(s)=\sum_a q_\pi(s,a) \pi(a|s) v π ( s ) = ∑ a q π ( s , a ) π ( a ∣ s )
v π ( s ) = ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ] \begin{aligned} v_\pi(s)=\sum_{a} \pi(a | s)\left[\sum_{r} p(r | s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} | s, a\right) v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} v π ( s ) = a ∑ π ( a ∣ s ) [ r ∑ p ( r ∣ s , a ) r + γ s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ ) ]
所以,q π ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) q_\pi(s,a) = \sum_{r} p(r | s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} | s, a\right) v_{\pi}\left(s^{\prime}\right) q π ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ )
实际意义是:在当前状态s下采取动作 a 所获得的均值,加上 γ \gamma γ
引入 action value 后,对于 state value 实际意义的解释:在当前状态s下,根据策略π \pi π
state value 和 action value 可以互相转化。
State value: v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s)=E[G_t|S_t=s] v π ( s ) = E [ G t ∣ S t = s ] Action value: q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=E[G_t|S_t=s,A_t=a] q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] State value 是 action value 的根据策略π \pi π v π ( s ) = ∑ a π ( a ∣ s ) q ( s , a ) v_\pi(s)=\sum_a \pi(a|s)q(s,a) v π ( s ) = ∑ a π ( a ∣ s ) q ( s , a ) The Bellman equation (elementwise form and matrix-vector form) 求解 the Bellman equation (2种方法)  由此可以推导出一个多步的trajectory:
由此可以推导出一个多步的trajectory: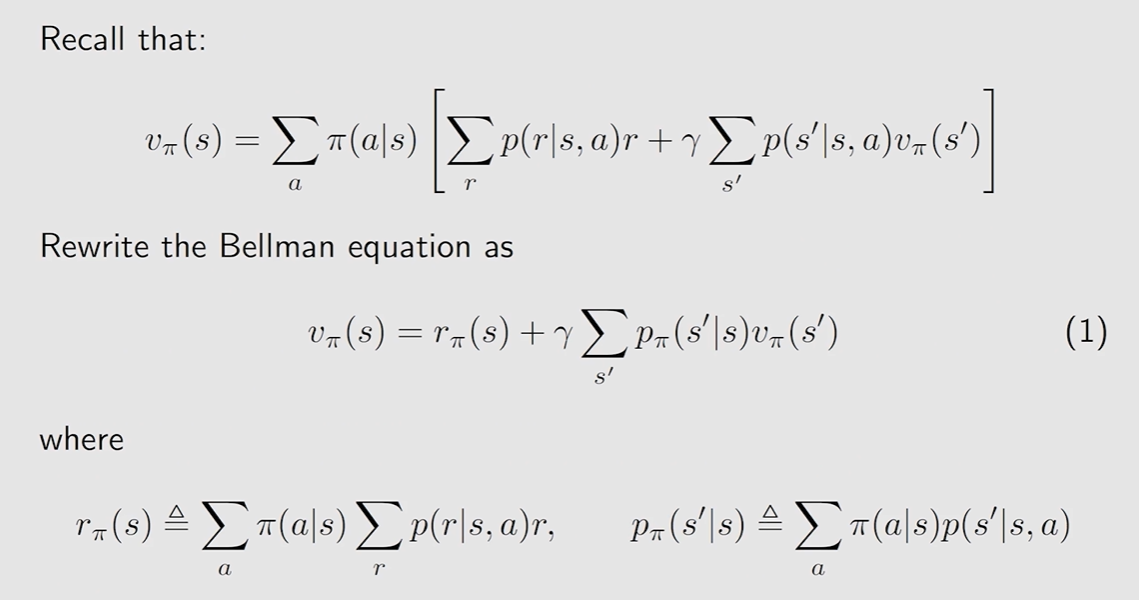 此时,对于所有状态,对应的 Bellman equation 为
此时,对于所有状态,对应的 Bellman equation 为