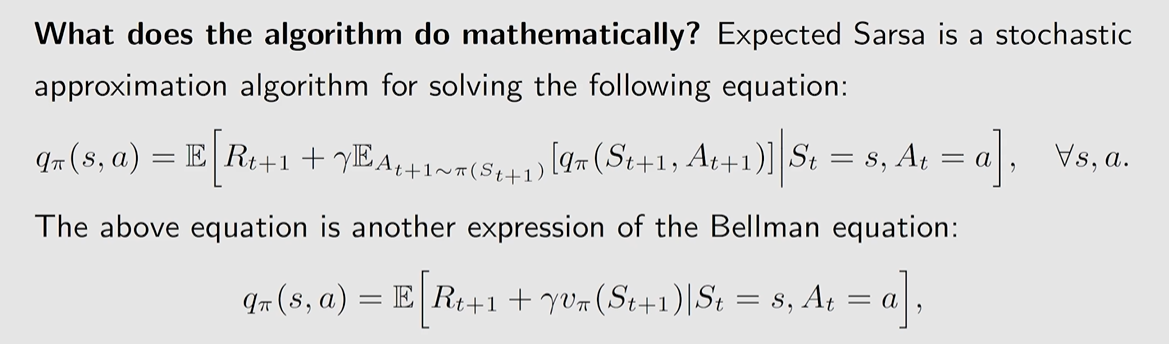考虑一个复杂的均值估计问题: 计算
ω=E[R+γv(X)],
其中, R, X 均是随机变量,γ 是常数,v(⋅) 表示一个函数。
显然我们仍然可以通过 RM 算法进行求解,假设我们可以得到有关随机变量 R, X 的采样 {x},{r}
g(w)g~(w,η)=w−E[R+γv(X)]=w−[r+γv(x)]=(w−E[R+γv(X)])+(E[R+γv(X)]−[r+γv(x)])≐g(w)+η
因此,我们可以将该问题定义为一个 root-finding 问题: g(w)=0.
相应的 RM 算法为:
wk+1=wk−αkg~(wk,ηk)=wk−αk[wk−[rk+γv(xk)]]
求解给定策略 π 的 state value,这样就可以与 policy improvement 结合去寻找最优策略。
算法所需的数据(experience):
根据给定的策略 π 所生成的数据 (s0,r1,s1,…,st,rt+1,st+1,…) or {(st,rt+1,st+1)}
相应的算法是:
vt+1(st)vt+1(s)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]]=vt(s),∀s=st,
其中 t=0,1,2,…, vt(st)是关于 vπ(st) 的估计。
new estimatevt+1(st)=current estimatevt(st)−αt(st)[vt(st)−TD target vtˉ[rt+1+γvt(st+1)]]TD error δt
TD 算法是用来求解一个 给定策略 π 的 Bellman equation.
根据 state value 的定义,对于策略 π 的 state value
vπ(s)=E[R+γG∣S=s],s∈S
其中 G 是 discounted return。
E[G∣S=s]=a∑π(a∣s)s′∑p(s′∣s,a)vπ(s)=E[vπ(S′)∣S=s]
因此,我们可以写出 Bellman equation 的新形式,称为 Bellman expection equation
vπ(s)=E[E+γvπ(S′)∣S=s],s∈S



Sarsa (state-action-reward-state-action)
Sarsa 算法其目的是用于直接估计 action value, 从而可以在 policy improvement 中直接根据 action value 进行更新即可。
Sarsa 算法同样是来求解 Bellman equation:
qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a
假设我们具有 some experience {(st,at,rt+1,st+1,at+1)}
对应的 Sarsa 算法如下来进行估计 action value:
qt+1(st,at)qt+1(s,a)=qt(sa,at)−αt(st,at)[qt(sa,at)−[rt+1+γqt(st+1,at+1)]]=qt(s,a),∀(s,a)=(st,at)
其中 t=0,1,2,…, qt(st,at) 是qπ(st,at)的估计。
收敛性情况
 20240817000114
20240817000114伪代码
 20240817000134
20240817000134 20240817000230
20240817000230 20240817000500
20240817000500 20240817000601
20240817000601 20240817000642
20240817000642 20240817000331
20240817000331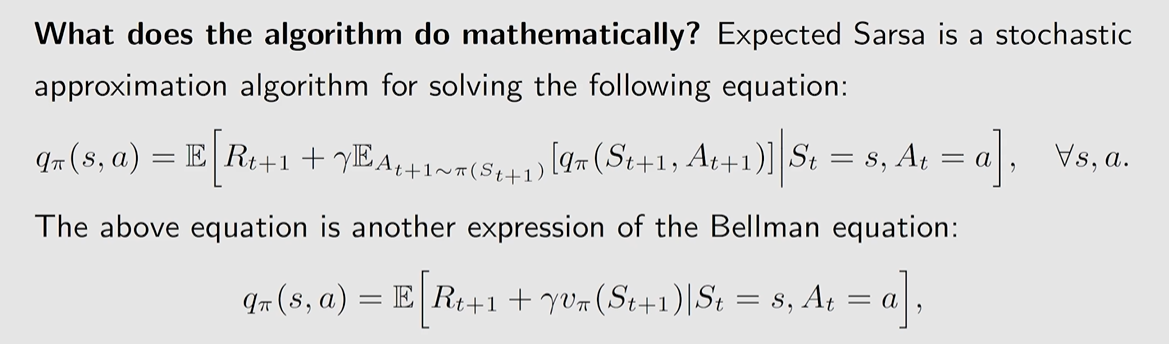 20240817000409
20240817000409Q-learning 算法是用来解决 action value 形式下的贝尔曼最优公式 (Bellman optimality equation in terms of action value)
q(s,a)=E[Rt+1+γamaxq(St+1,a)∣St=s,At=a],∀s,a
Q-learning 直接估计的是 optimal action value,因此不需要进行 policy improvement。
qt+1(st,at)qt+1(s,a)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γa∈Amaxqt(st+1,a)]]=qt(s,a),∀(s,a)=(st,at)
- behavior policy: 是用来与环境进行交互,从而生成经验数据的策略
- target policy: 是我们不断进行更新的策略,最终优化的策略
该算法中 behavior policy 和 target policy 是一致的,即我通过这个策略与环境进行交互生成一系列经验,在通过经验来更新这个策略。
该算法中 behavior policy 和 target policy 是不同的,即我通过一个策略与环境进行交互生成一系列经验。再通过这些经验来不断改进更新另一个策略,这另一个策略会更新到最优的策略。
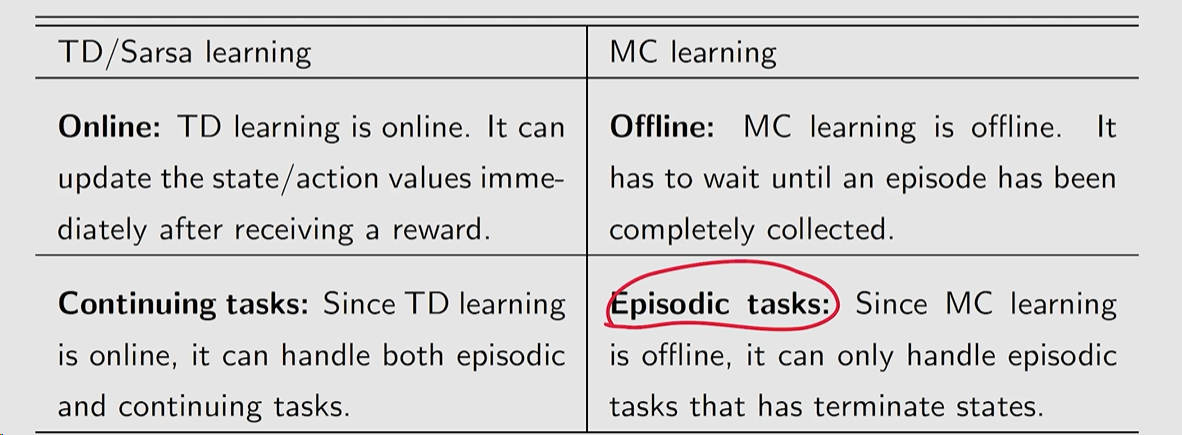
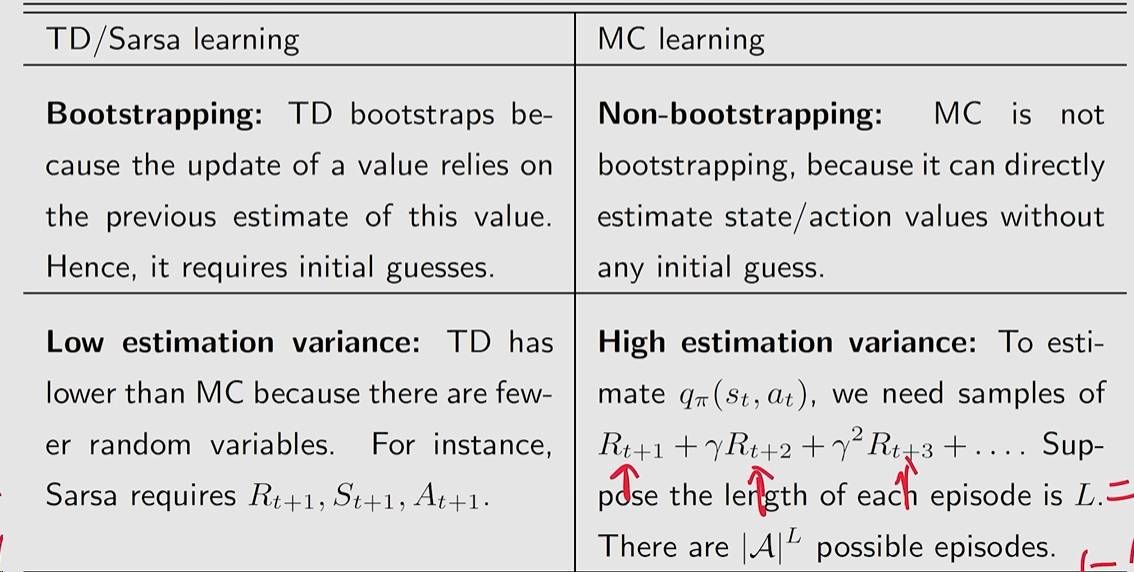
Sarsa,MC 是 on-policy 的
Q-learning 是 off-policy 的
因为 Q-learning 是 off-policy 的,因此,如果我们强制让 target policy 与 behavior ppolicy 一致也是可以的,此时也可以是 on-policy 的。
 20240818182057
20240818182057此时 target policy 就不需要是 ϵ−greedy 策略了,因为不需要 target policy 进行生成数据。
 20240818181917
20240818181917 20240818182301
20240818182301 20240818182231
20240818182231