2019 IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY
A novel framework is proposed for quality of experience driven deployment and dynamic movement of multiple unmanned aerial vehicles (UAVs). 过去研究大多没有基于用户的移动(movement of users)来考虑无人机的机动性,更多地是考虑多架无人机的二维部署或单架无人机在地面用户保持静止情况下的部署。 考虑QoE, 而不是仅考虑吞吐量(throughput),即需要考虑地面不同用户的具体需求。(QoE is invoked for demonstrating the users’ satisfaction, and it is supposed to be considered in UAV-assisted wireless networks) 该文设计的是3D部署,过去研究主要考虑的是2D部署。 提出了一个理想的由QoE驱动的多无人机协助通信框架。该框架将无人机部署在三维空间内,以 mean opinion score(MOS) 为指标。通过优化无人机的部署和动态移动来解决总用户MOS最大化问题。 提出解决总用户MOS最大化问题的三步骤: 通过GAK-mean算法获得初始单元划分。 设计一种基于 q-learning 的部署方法,在初始时间假设用户处于静止下不断调整 UAVs 3D位置进行优化处理。 设计一种基于 q-learning 的无人机3D动态运动设计算法。 该文基于q-learning的方案来解决无人机的NP-hard 3D部署和移动问题,并与传统的基于遗传的学习算法进行对比。 该文提出的算法具较快的收敛性,与K-means和IGK算法比具有较低的复杂度。 考虑无人机辅助无线网络的下行链路传输(down-link transmission),即无人机作为空中基站。
对于指定区域,会将其划分为N N N K = K 1 , … , K N K={K_1,\dots,K_N} K = K 1 , … , K N K N K_N K N N N N N ∈ 1 , 2 , … , N N\in{1,2,\dots,N} N ∈ 1 , 2 , … , N
每个用户只能属于一个集群,K n ∩ K n ′ = ϕ , n ′ ≠ n , K_n\cap K_{n^{'}}=\phi, n^{'}\ne n, K n ∩ K n ′ = ϕ , n ′ = n ,
在任意时刻t,同一无人机通过FDMA 同时为同一集群中的多个用户提供服务
对于用户k n ∈ K n k_n\in K_n k n ∈ K n w k n = [ x k n ( t ) , y k n ( t ) ] T ∈ R 2 × 1 w_{k_n}=[x_{k_n}(t),y_{k_n}(t)]^T\in R^{2\times1} w k n = [ x k n ( t ) , y k n ( t ) ] T ∈ R 2 × 1
对于无人机n n n (飞行速度恒定) ,其垂直高度表示为h n ( t ) ∈ [ h m i n , h m a x ] , 0 ≤ t ≤ T s h_n(t)\in[h_{min},h_{max}], 0\leq t\leq T_s h n ( t ) ∈ [ h min , h ma x ] , 0 ≤ t ≤ T s q n ( t ) = [ x n ( t ) , y n ( t ) ] T ∈ R 2 × 1 , 0 ≤ t ≤ T s q_n(t)=[x_n(t),y_n(t)]^T\in R^{2\times 1}, 0\leq t\leq T_s q n ( t ) = [ x n ( t ) , y n ( t ) ] T ∈ R 2 × 1 , 0 ≤ t ≤ T s
无人机n n n k n k_n k n t t t
d k n = h n 2 ( t ) + [ x n ( t ) − x k n ( t ) ] 2 + [ y n ( t ) − y k n ( t ) ] 2 d_{k_n}=\sqrt{{h_{n}^2(t)+[x_n(t)-x_{k_n}(t)]^2+[y_n(t)-y_{k_n}(t)]^2}} d k n = h n 2 ( t ) + [ x n ( t ) − x k n ( t ) ] 2 + [ y n ( t ) − y k n ( t ) ] 2
无人机往往有更高的LoS链接概率,该文中表示为:
P L o S ( θ k n ) = b 1 ( 180 π θ k n − ζ ) b 2 P N L o S = 1 − P L o S P_{LoS}(\theta_{k_n})=b_1(\frac{180}{\pi}\theta_{k_n}-\zeta)^{b_2} \\ P_{NLoS}=1-P_{LoS} P L o S ( θ k n ) = b 1 ( π 180 θ k n − ζ ) b 2 P N L o S = 1 − P L o S
其中θ k n ( t ) = s i n − 1 [ h n ( t ) d k n ( t ) ] \theta_{k_n}(t)=sin^{-1}[\frac{h_n{(t)}}{d_{k_n(t)}}] θ k n ( t ) = s i n − 1 [ d k n ( t ) h n ( t ) ] b 1 , b 2 , ζ b_1, b_2, \zeta b 1 , b 2 , ζ n n n h n ( t ) h_n(t) h n ( t )
在时间t t t n n n k n k_n k n
g k n ( t ) = K 0 − 1 d k n − α [ t ] ( P L o s μ L o S + P N L o s μ N L o S ) − 1 g_{k_n}(t)={K_0}^{-1}{d_{k_n}}^{-\alpha}[t](P_{Los}\mu_{LoS}+P_{NLos}\mu_{NLoS})^{-1} g k n ( t ) = K 0 − 1 d k n − α [ t ] ( P L os μ L o S + P N L os μ N L o S ) − 1
其中K 0 = ( 4 π f c c ) 2 K_0=(\frac{4\pi f_c}{c})^2 K 0 = ( c 4 π f c ) 2 α \alpha α μ L o S , μ N L o S \mu_{LoS},\mu_{NLoS} μ L o S , μ N L o S f c f_c f c c c c
对于无人机n n n B n B_n B n ∣ K n ∣ \left | K_n \right | ∣ K n ∣ B k n = B n / K n B_{k_n}=B_n/K_n B k n = B n / K n p k n = P m a x / K n p_{k_n}=P_{max}/K_n p k n = P ma x / K n
由于不同集群的频谱不同,可以减轻无人机对用户接收到的干扰。因此,在时刻t t t n n n k n k_n k n
Γ k n ( t ) = p k n g k n ( t ) σ 2 \Gamma_{k_n}(t)=\frac{p_{k_n}g_{k_n}(t)}{\sigma^2} Γ k n ( t ) = σ 2 p k n g k n ( t )
其中σ 2 = B k n N 0 \sigma^2=B_{k_n}N_0 σ 2 = B k n N 0 N 0 N_0 N 0
为了满足不同用户传输速率要求,对于用户k n k_n k n γ k n \gamma_{k_n} γ k n Γ ≥ γ k n \Gamma\geq \gamma_{k_n} Γ ≥ γ k n
由此,存在L e m m a 1 Lemma\ 1 L e mma 1
P m a x ≥ γ σ 2 K 0 d k n α ( t ) μ N L o S P_{max}\ge\gamma\sigma^{2}K_0{d_{k_n}}^{\alpha}(t)\mu_{NLoS} P ma x ≥ γ σ 2 K 0 d k n α ( t ) μ N L o S
根据香农定理: 信道容量C = B ∗ l o g ( 1 + S N ) C=B*log(1+\frac{S}{N}) C = B ∗ l o g ( 1 + N S ) k n k_n k n t t t r k n ( t ) r_{k_n}(t) r k n ( t ) r k n ( t ) = B k n l o g 2 [ 1 + p k n g k n ( t ) σ 2 ] r_{k_n}(t)=B_{k_n}log_2[1+\frac{p_{k_n}g_{k_n}(t)}{\sigma^2}] r k n ( t ) = B k n l o g 2 [ 1 + σ 2 p k n g k n ( t ) ]
P r o p o s i t i o n 1 : Proposition\ 1: P ro p os i t i o n 1 : n n n
d k n ( t ) s i n [ π 180 ( ζ + e M ( t ) ) ] ≤ h n ( t ) ≤ ( P m a x γ K 0 σ 2 μ L o S ) d_{k_n}(t)sin[\frac{\pi}{180}(\zeta+e^{M(t)})]\leq h_n(t)\leq(\frac{P_{max}}{\gamma K_0\sigma^2\mu_{LoS}}) d k n ( t ) s in [ 180 π ( ζ + e M ( t ) )] ≤ h n ( t ) ≤ ( γ K 0 σ 2 μ L o S P ma x )
其中
M ( t ) = l n ( S ( t ) ( μ L o S − μ N L o S ) − μ N L o S μ L o S − μ N L o S b 1 b 2 S ( t ) = P m a x γ K 0 σ 2 d k n α ( t ) M(t)=\frac{ln(\frac{\frac{S(t)}{(\mu_{LoS}-\mu_{NLoS})}-\frac{\mu{NLoS}}{\mu_{LoS}-\mu_{NLoS}}}{b_1}}{b_2} \\ \\ S(t)=\frac{P_max}{\gamma K_0\sigma^2{d_{k_n}}^{\alpha}(t)} M ( t ) = b 2 l n ( b 1 ( μ L o S − μ N L o S ) S ( t ) − μ L o S − μ N L o S μ N L o S S ( t ) = γ K 0 σ 2 d k n α ( t ) P m a x
P r o p o s i t i o n 1 Proposition\ 1 P ro p os i t i o n 1 高度 的必要条件。d k n ( t ) d_{k_n}(t) d k n ( t ) P m a x P_{max} P ma x
由于不同用户对于传输速率的需求是不同的,所以在无人机辅助通信网络中我们需要考虑QoE模型。
在该文中,采用MOS作为用户QoS衡量的标准,具体如下:
M O S k n ( t ) = ζ 1 M O S k n d e l a y ( t ) + ζ 2 M O S k n r a t e ( t ) MOS_{k_n}(t)=\zeta_1{MOS_{k_n}}^{delay}(t)+\zeta_2{MOS_{k_n}}^{rate}(t) MO S k n ( t ) = ζ 1 MO S k n d e l a y ( t ) + ζ 2 MO S k n r a t e ( t )
其中,ζ 1 , ζ 2 \zeta_1,\zeta_2 ζ 1 , ζ 2 ζ 1 + ζ 2 = 1 \zeta_1+\zeta_2=1 ζ 1 + ζ 2 = 1
根据MOS数值,共划分5个等级: excellent(4.5) very good(2~3.5) fair(1~2) poor(1)。
在该文中考虑的是网页浏览应用传输情况,因此M O S k n d e l a y ( t ) {MOS_{k_n}}^{delay}(t) MO S k n d e l a y ( t )
M O S k n ( t ) = − C 1 l n [ d ( r k n ( t ) ) ] + C 2 MOS_{k_n}(t)=-C_1ln[d(r_{k_n}(t))]+C_2 MO S k n ( t ) = − C 1 l n [ d ( r k n ( t ))] + C 2
d ( r k n ( t ) ) d(r_{k_n}(t)) d ( r k n ( t )) M O S k n ( t ) MOS_{k_n}(t) MO S k n ( t ) 1 − 4.5 1-4.5 1 − 4.5 C 1 C_1 C 1 C 2 C_2 C 2
d ( r k n ( t ) ) = 3 R T T + F S r k n ( t ) + L ( M S S r k n ) + R T T − 2 M S S ( 2 L − 1 ) r k n ( t ) d(r_{k_n}(t))=3RTT+\frac{FS}{r_{k_n}(t)}+L(\frac{MSS}{r_{k_n}})+RTT-\frac{2MSS(2^L-1)}{r_{k_n}(t)} d ( r k n ( t )) = 3 RTT + r k n ( t ) FS + L ( r k n MSS ) + RTT − r k n ( t ) 2 MSS ( 2 L − 1 )
其中,RTT[s]表示round trip time(数据包从发送端-接收端-发送端的时间),FS[bit]是网页大小,MSS[bit]是最大报文长度,L = m i n [ L 1 , L 2 ] L=min[L_1,L_2] L = min [ L 1 , L 2 ]
L 1 = l o g 2 ( r k n R T T M S S + 1 ) − 1 , L 2 = l o g 2 ( F S 2 M S S + 1 ) − 1 L_1=log_2(\frac{r_{k_n}RTT}{MSS}+1)-1,\quad L_2=log_2(\frac{FS}{2MSS}+1)-1 L 1 = l o g 2 ( MSS r k n RTT + 1 ) − 1 , L 2 = l o g 2 ( 2 MSS FS + 1 ) − 1
用户r k n r_{k_n} r k n T s T_s T s
M O S r k n = ∑ t = 0 T s M O S k n ( t ) MOS_{r_{k_n}}=\sum_{t=0}^{T_s}MOS_{k_n}(t) MO S r k n = t = 0 ∑ T s MO S k n ( t )
假设功率Q = q n ( t ) , 0 ≤ t ≤ T s Q={q_n(t),0\leq t\leq T_s} Q = q n ( t ) , 0 ≤ t ≤ T s H = h n ( t ) , 0 ≤ t ≤ T s H={h_n(t),0\leq t\leq T_s} H = h n ( t ) , 0 ≤ t ≤ T s
本文目的是优化无人机在每个时隙的位置,从而最大化所有用户的总MOS值。具体表述如下:
max C , Q , H M O S t o t a l = ∑ n = 1 N ∑ k n = 1 K n ∑ t = 0 T s M O S k n ( t ) s . t . K n ∩ K n ′ = ϕ , n ′ ≠ n , ∀ n , h m i n ≤ h n ( t ) ≤ h m a x , ∀ t , ∀ n , Γ k n ( t ) ≥ γ k n , ∀ t , ∀ k n , ∑ k n = 1 K n p k n ( t ) ≤ P m a x , ∀ t , ∀ k n , p k n ( t ) ≥ 0 , ∀ k n , ∀ t , \begin{array}{l} \underset{C,Q,H}{\max} MOS_{total}=\sum_{n=1}^N\sum_{k_n=1}^{K_n}\sum_{t=0}^{T_s}MOS_{k_n}(t) \\ \\ s.t.\quad K_n\cap K_{n^{'}}=\phi ,n^{'}\neq n, \forall n, \\ \\ h_{min}\leq h_n(t)\leq h_{max},\forall t, \forall n, \\ \\ \Gamma_{k_n(t)}\geq \gamma_{k_n}, \forall t, \forall k_n, \\ \\ \sum_{k_n=1}^{K_n}p_{k_n}(t)\leq P_{max}, \forall t, \forall k_n, \\ \\ p_{k_n(t)}\geq 0, \forall k_n, \forall t, \end{array} C , Q , H max MO S t o t a l = ∑ n = 1 N ∑ k n = 1 K n ∑ t = 0 T s MO S k n ( t ) s . t . K n ∩ K n ′ = ϕ , n ′ = n , ∀ n , h min ≤ h n ( t ) ≤ h ma x , ∀ t , ∀ n , Γ k n ( t ) ≥ γ k n , ∀ t , ∀ k n , ∑ k n = 1 K n p k n ( t ) ≤ P ma x , ∀ t , ∀ k n , p k n ( t ) ≥ 0 , ∀ k n , ∀ t ,
该优化问题是一个non-convex问题,因为目标函数对于无人机的3D坐标是非凸的。 总用户的MOS取决于无人机的发射功率、数量和位置(水平位置和高度)。 考虑以下场景,将上述优化问题简化:
无人机n n n 静态 的。优化问题 简化为区域分割问题 。
描述如下: 但即使仅考虑用户聚类,该问题依然是NP-hard问题
max C , Q , H M O S t o t a l = ∑ n = 1 N ∑ k n = 1 K n M O S k n ( t ) s . t . K n ∩ K n ′ = ϕ , n ′ ≠ n , ∀ n , h m i n ≤ h n ( t ) ≤ h m a x , ∀ t , ∀ n , Γ k n ( t ) ≥ γ k n , ∀ t , ∀ k n , ∑ k n = 1 K n p k n ( t ) ≤ P m a x , ∀ t , ∀ k n , p k n ( t ) ≥ 0 , ∀ k n , ∀ t , \begin{array}{l} \underset{C,Q,H}{\max} MOS_{total}=\sum_{n=1}^N\sum_{k_n=1}^{K_n}MOS_{k_n}(t) \\ \\ s.t.\quad K_n\cap K_{n^{'}}=\phi ,n^{'}\neq n, \forall n, \\ \\ h_{min}\leq h_n(t)\leq h_{max},\forall t, \forall n, \\ \\ \Gamma_{k_n(t)}\geq \gamma_{k_n}, \forall t, \forall k_n, \\ \\ \sum_{k_n=1}^{K_n}p_{k_n}(t)\leq P_{max}, \forall t, \forall k_n, \\ \\ p_{k_n(t)}\geq 0, \forall k_n, \forall t, \end{array} C , Q , H max MO S t o t a l = ∑ n = 1 N ∑ k n = 1 K n MO S k n ( t ) s . t . K n ∩ K n ′ = ϕ , n ′ = n , ∀ n , h min ≤ h n ( t ) ≤ h ma x , ∀ t , ∀ n , Γ k n ( t ) ≥ γ k n , ∀ t , ∀ k n , ∑ k n = 1 K n p k n ( t ) ≤ P ma x , ∀ t , ∀ k n , p k n ( t ) ≥ 0 , ∀ k n , ∀ t ,
无人机-用户关联策略(用户区域划分算法)
采用基于遗传算法的GAK-means算法 由于特定用户的MOS与该用户与无人机之间的距离有关,因此GAK-means可以视为获得无人机部署的低复杂度方案 。
根据N个用户,根据遗传算法找到C N C_N C N 将无人机部署在每个中心内,再将用户划分给距离最近的无人机 重复步骤,再找到新的簇的各中心,再根据欧几里得距离重新划分,直到各个簇的成员没有太大变化,划分完毕。
无人机3D部署算法
根据所给定的用户划分情况,目标是获得无人机的最佳3D位置,来最大化MOS总和 。 由于GAK-means的优化目标是最小化无人机与对应集群用户的欧氏距离,MOS主要是有关传输速率r k n r_{k_{n}} r k n
采用Q-learning算法
智能体(agent): U A V n , n ∈ N = { 1 , 2 , … , N } UAV\ n, n\in \mathbb{N}=\{1,2,\dots,N\} U A V n , n ∈ N = { 1 , 2 , … , N }
状态(state): 对于每个智能体,其状态为其3D坐标,定义为ξ = ( x U A V , y U A V , h U A V ) \xi=(x_{UAV},y_{UAV},h_{UAV}) ξ = ( x U A V , y U A V , h U A V )
状态空间(state space S S S 离散化 空间坐标,即x U A V : { 0 , 1 , … , X d } , y U A V : 0 , 1 , … , Y d , h U A V : { h m i n , … , h m a x } x_{UAV}:\{0,1,\dots,X_d\},\ y_{UAV}:{0,1,\dots,Y_d},\ h_{UAV}:\{h_{min},\dots,h_{max}\} x U A V : { 0 , 1 , … , X d } , y U A V : 0 , 1 , … , Y d , h U A V : { h min , … , h ma x } ( X D + 1 ) × ( Y d + 1 ) × ( h m a x − h m i n + 1 ) (X_D+1)\times(Y_d+1)\times(h_{max}-h_{min}+1) ( X D + 1 ) × ( Y d + 1 ) × ( h ma x − h min + 1 )
动作空间(action space): 每次无人机会根据当前状态s t ∈ S s_t\in S s t ∈ S J J J a t ∈ A a_t\in A a t ∈ A r t r_t r t s t + 1 s_{t+1} s t + 1 7 个方向。 ( 1 , 0 , 0 ) (1,0,0) ( 1 , 0 , 0 ) ( − 1 , 0 , 0 ) (-1,0,0) ( − 1 , 0 , 0 ) ( 0 , 1 , 0 ) (0,1,0) ( 0 , 1 , 0 ) ( 0 , − 1 , 0 ) (0,-1,0) ( 0 , − 1 , 0 ) ( 0 , 0 , 1 ) (0,0,1) ( 0 , 0 , 1 ) ( 0 , 0 , − 1 ) (0,0,-1) ( 0 , 0 , − 1 ) ( 0 , 0 , 0 ) (0,0,0) ( 0 , 0 , 0 )
状态转换模型: 当执行动作a t a_t a t s t s_t s t s t + 1 s_{t+1} s t + 1 r t r_t r t p ( s t + 1 , r t ∣ s t , a t ) p(s_{t+1}, r_t|s_t, a_t) p ( s t + 1 , r t ∣ s t , a t )
G t = E [ ∑ n = 0 ∞ β n r t + n ] G_t=E[\sum_{n=0}^{\infin}\beta^nr_{t+n}] G t = E [ n = 0 ∑ ∞ β n r t + n ]
奖励(reward): 如果agent在当前时刻t所执行的动作能够提高总MOS,则无人机将获得正奖励。否则,agent将获得负奖励。
x t = { 1 , i f M O S n e w > M O S o l d − 0.1 , i f M O S n e w = M O S o l d − 1 , i f M O S n e w < M O S o l d x_t= \begin{cases} 1,&if\quad MOS_{new}>MOS_{old} \\ -0.1,&if\quad MOS_{new}=MOS_{old} \\ -1,&if\quad MOS_{new}<MOS_{old} \end{cases} x t = ⎩ ⎨ ⎧ 1 , − 0.1 , − 1 , i f MO S n e w > MO S o l d i f MO S n e w = MO S o l d i f MO S n e w < MO S o l d
具体代码:(策略为贪心策略)
算法1 个人理解:
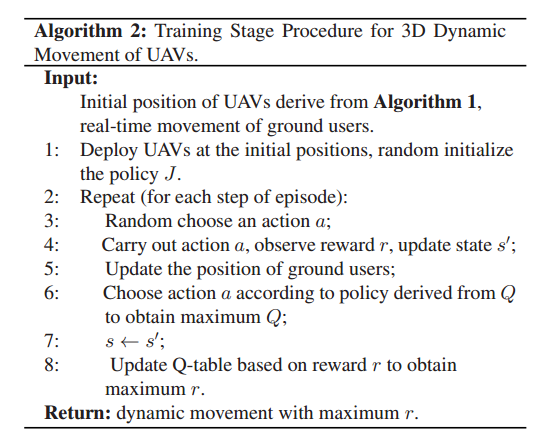
通过K-means来划分各个无人机所管理的用户簇。无人机的位置初始化也是随机部署的 但每个无人机所管理的用户不同,其目标也应该不一样,不能用同一个Q-table管理,这里是每个无人机都有一张自己的Q-table,来进行迭代? 还是同一张Q-table,只不过根据区域划分,不同的无人机agent的Q(s,a)的s是有范围的?(个人感觉是这个) 最终输出的结果,应该是无人机最终停的位置即是部署的最佳位置(因为q-learning是优化长期目标),发现在该位置静止是最优的,表示是最佳部署位置。 最终输出结果,是根据Q-table来找出对应q(s,a)当a为静止时,最大的q(s,a)值,对应s就是UAV的部署位置 考虑用户在每个时隙移动的情况,由于用户在每个时隙都处于漫游状态,因此随着用户位置的变化,每个集群中无人机的最优位置也会发生变化,无人机需要进行移动。
在本文中不考虑用户移动到其他集群的情况 因为在不考虑用户自由穿梭集群的情况,对于动作空间而言,仅需要考虑无人机的7个移动方向即可;但若考虑集群情况,动作空间包含两个部分:选择移动方向和选择关联用户。设无人机总数为N N N ∣ K n ∣ |K_n| ∣ K n ∣ 2 N ∑ n = 1 N ∣ K n ∣ 2N\sum_{n=1}^{N}|K_n| 2 N ∑ n = 1 N ∣ K n ∣ ∑ n = 1 N ∣ K n ∣ \sum_{n=1}^{N}|K_n| ∑ n = 1 N ∣ K n ∣ 2 N 2N 2 N 7 + 2 N ∑ n = 1 N ∣ K n ∣ 7+2N\sum_{n=1}^{N}|K_n| 7 + 2 N ∑ n = 1 N ∣ K n ∣
1.用户漫游模型 在设计无人机的移动之前,需考虑用户的移动性,这里有多种mobility modles可选择,如a deterministic approach, a hybrid approach, and a random walk model. 在本文中,采用的是the random walk model(Markovian mobility model) 每个用户的移动方向均匀分布在左、右、前、后四个方向。 用户的速度设为[ 0 , c m a x ] [0,c_{max}] [ 0 , c ma x ] c m a x c_{max} c ma x
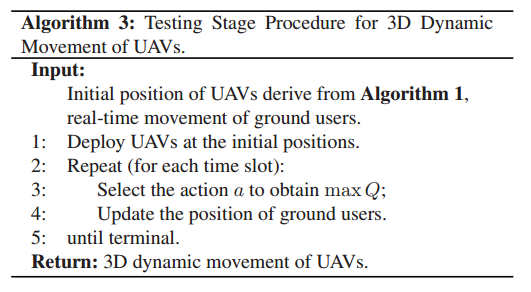
2.基于q-learning的移动算法 与基于q-learning的部署算法不同的是,在此情况下,状态除了要考虑无人机的3D位置外,还需要考虑所有用户的2D位置。即ξ = { x U A V , y U A V , h U A V , x u s e r , y u s e r } \xi=\{x_{UAV},y_{UAV},h_{UAV},x_{user},y_{user}\} ξ = { x U A V , y U A V , h U A V , x u ser , y u ser } ( x u s e r , y u s e r ) (x_{user}, y_{user}) ( x u ser , y u ser ) ( x U A V , y U A V , h U A V ) (x_{UAV}, y_{UAV}, h_{UAV}) ( x U A V , y U A V , h U A V )
训练阶段:
测试阶段: